Selección de Modelos¶

Ya teniendo todos los ingredientes a nuestra disposición es hora de cocinarlos juntos y escoger la mejor receta. Por receta nos referimos al mejor modelo para tu problema y datos asociados.

Estimadores¶

Ya sabemos que scikit-learn nos provee de múltiples algoritmos y modelos de Machine Learning, que oficialmente son llamados estimadores (estimators). Cada estimator puede ser ajustado (o coloquialmente, fiteado) utilizando los datos adecuados.

Ppara motivar, la Regresión Ridge es un tipo de regresión que agrega un parámetro de regularización, en particular, busca minimizar la suma de residuos pero penalizada, es decir:

\[ \min_\beta \vert \vert y - X \beta \vert \vert_2^2 + \alpha \vert \vert \beta \vert \vert_2^2 \]

El hiper-parámetro \(\alpha > 0\) es usualmente conocido como parámetro penalización ridge. En realidad, en la literatura estadística se denota con \(lambda\), pero como en python el nombre lambda está reservado para las funciones anónimas, scikit-learn optó por utilizar otra letra griega. La regresión ridge es una alternativa popularpara sobrellevar el problema de colinealidad.

En scikit-learn.linear_models se encuentra el estimador Ridge.

import numpy as np

from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split

from sklearn.datasets import load_boston

# load_boston?

# Ridge??

X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

rr_est = Ridge(alpha=0.1)

type(rr_est)

sklearn.linear_model._ridge.Ridge

Típicamente el método fit acepta dos inputs:

La matriz de diseño X, arreglo bidimensional que generalmente es de tamaño (n_samples, n_features).
Los valores target y.
- En tareas de regresión corresponden a números reales.
- En tareas de clasificación corresponden a categorías.
- Para aprendizaje no-supervisado este input no es necesario.

rr_est.fit(X, y)

Ridge(alpha=0.1)

Luego de ajustar podemos obtener algunos atributos, en particular, esta regresión ajustó los atributos coef_ y intercept_.

rr_est.coef_

array([-1.07473720e-01,  4.65716366e-02,  1.59989982e-02,  2.67001859e+00,
       -1.66846452e+01,  3.81823322e+00, -2.69060598e-04, -1.45962557e+00,
        3.03515266e-01, -1.24205910e-02, -9.40758541e-01,  9.36807461e-03,
       -5.25966203e-01])

rr_est.intercept_

35.693653711658996

El método predict necesita un arreglo bidimensional como input. Para ejemplificar podemos utilizar la misma data de entrenamiento.

rr_est.predict(X)[:10]

array([30.04164633, 24.99087654, 30.56235738, 28.65418856, 27.98110937,
       25.28351105, 22.99401212, 19.49937732, 11.46728387, 18.90419332])

En un flujo estándar ajustaríamos con los datos de entrenamiento, luego se predice en los datos de test y finalmente se obtiene alguna métrica, por ejemplo para un caso de regresión, el error cuadrático medio o incluso el mismo coeficiente de determinación.

rr_est.fit(X_train, y_train)

Ridge(alpha=0.1)

y_pred = rr_est.predict(X_test)

from sklearn.metrics import mean_squared_error, r2_score

Estas métricas generalmente tienen como argumento un vector con los datos reales y un vector con los datos predecidos/estimados.

mean_squared_error(y_test, y_pred)

22.142232974238876

r2_score(y_test, y_pred)

0.6838049959091362

Sin embargo, es importante recordar que los estimadores tienen métodos de scoring por defecto.

Modelos de regresión utilizan por defecto \(R^2\) (coeficiente de determinación) como score.
Modelos de clasificación utilizan por defecto el accuracy como score.

El método es score y como argumentos necesita un arreglo bidimensional y un vector unidimensional, típicamente asociados a los conjuntos de test. Internamente el método hace la estimación del arreglo bidimensional entregado.

rr_est.score(X_test, y_test)

0.6838049959091362

Pre-Procesamiento¶

En el flujo de trabajo típico de un proyecto de machine learning es usual procesar y transformar los datos. En scikit-learn el pre-procesamiento y transformación siguen la misma API que los objetos estimators, pero que se denotan como transformers. Sin embargo, estos no poseen un método predict pero si uno de transformación, transform.

Motivaremos con la típica estandarización.

from sklearn.preprocessing import StandardScaler

# StandardScaler?

Usualmente se ajusta y transformar los mismos datos, por lo que se aplican los métodos concatenados.

X.shape

(506, 13)

std_transformer = StandardScaler()

std_transformer.fit(X).transform(X)

array([[-0.41978194,  0.28482986, -1.2879095 , ..., -1.45900038,
         0.44105193, -1.0755623 ],
       [-0.41733926, -0.48772236, -0.59338101, ..., -0.30309415,
         0.44105193, -0.49243937],
       [-0.41734159, -0.48772236, -0.59338101, ..., -0.30309415,
         0.39642699, -1.2087274 ],
       ...,
       [-0.41344658, -0.48772236,  0.11573841, ...,  1.17646583,
         0.44105193, -0.98304761],
       [-0.40776407, -0.48772236,  0.11573841, ...,  1.17646583,
         0.4032249 , -0.86530163],
       [-0.41500016, -0.48772236,  0.11573841, ...,  1.17646583,
         0.44105193, -0.66905833]])

Sin embargo, muchos de estos objetos (si es que no es la totalidad de ellos), poseen el método fit_transform.

X_scaled = std_transformer.fit_transform(X)

Verificamos que el promedio es prácticamente cero.

np.mean(X_scaled, axis=0)

array([-8.78743718e-17, -6.34319123e-16, -2.68291099e-15,  4.70199198e-16,
        2.49032240e-15, -1.14523016e-14, -1.40785495e-15,  9.21090169e-16,
        5.44140929e-16, -8.86861950e-16, -9.20563581e-15,  8.16310129e-15,
       -3.37016317e-16])

np.allclose(np.mean(X_scaled, axis=0), 0)

True

Y que la desvicación estándar es unitaria.

np.std(X_scaled, axis=0)

array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

np.allclose(np.std(X_scaled, axis=0), 1)

True

De todas formas existen más formas de procesar tus datos, la sintáxis es similar e incluso pueden terner sus propios parámetros.

from sklearn.preprocessing import Normalizer

norm_transformer = Normalizer(norm="l2")
X_normalized = norm_transformer.fit_transform(X)

np.linalg.norm(X_normalized, axis=1, ord=2)

array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

np.allclose(np.linalg.norm(X_normalized, axis=1, ord=2), 1)

True

Pipelines¶

Scikit-learn nos permite combinar transformers y estimators uniéndolos a través de “tuberías”, objeto denotado como pipeline. Nuevamente, la API es consistente con un estimator, tanto como para ajustar como para predecir.

from sklearn.pipeline import make_pipeline

pipe = make_pipeline(
    StandardScaler(),
    Ridge(alpha=0.1)
)

pipe.fit(X_train, y_train)

Pipeline(steps=[('standardscaler', StandardScaler()),
                ('ridge', Ridge(alpha=0.1))])

pipe.predict(X_test)[:10]

array([28.83639192, 36.00279792, 15.09483565, 25.22983181, 18.87788941,
       23.21453831, 17.59519315, 14.30885051, 23.04885263, 20.62241378])

mean_squared_error(pipe.predict(X_test), y_test)

22.10050797409458

Evaluación de Modelos¶

Ya sabemos que ajustar un modelo con datos conocidos no implica que se comportará de buena manera con datos nuevos, por lo que tenemos herramientas como cross validation para evaluar los modelos con los datos conocidos.

from sklearn.model_selection import cross_validate

result = cross_validate(rr_est, X_train, y_train, cv=10)  # defaults to 5-fold CV

result["test_score"]

array([0.78222779, 0.70243923, 0.5550581 , 0.73853666, 0.82857777,
       0.69870779, 0.80564306, 0.71696332, 0.78792705, 0.54451998])

Búsqueda de Hiper-parámetros¶

Para el caso de la regeresión ridge, el parámetro de penalización es un hiper-parámetro que necesita ser escogido con algún procedimiento. Aunque no lo creas, scikit-learn también provee herramientas para escoger automáticamente este tipo de hiper-parámetros.

Por ejemplo GridSearchCV realiza una búsqueda exhaustiva entre los posibles valores especificados para los hiper-parámetros.

from sklearn.model_selection import GridSearchCV

param_grid = {
    "alpha": np.arange(0, 1, 0.1)
}

search = GridSearchCV(
    estimator=rr_est,
    param_grid=param_grid
)

search.fit(X_train, y_train)

GridSearchCV(estimator=Ridge(alpha=0.1),
             param_grid={'alpha': array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])})

search.best_params_

{'alpha': 0.0}

El objeto search ahora es equivalente a un estimator Ridge pero con los mejores parámetros encontrados (alpha = 0).

search.score(X_test, y_test)

0.6844267283527126

Selección de Modelos¶

Ya hemos comentado que lo importante a la hora de evaluar el desempeño de un modelo es a través de métricas en el conjunto de test. Sin embargo, si además es necesario ajustar hiper-parámetros la típica partición train/test este se podría modificar (tunear) hasta obtener el mejor score en el conjunto test.

Una alternativa es dividir los datos en tres conjuntos, train, validation y test, donde el conjunto de validación es para obtener los mejores hiper-parámetros. El problema que viene inmediatamente con este enfoque es que en ocasiones cuando no hay suficiente volumen de datos el conjunto de entrenamiento no es lo suficientemente grande como para que el algoritmo aprenda y generalice de buena manera. En contextos de redes neuronales, cuando los datos no son un problema, este enfoque funciona de maravilla, pues además ajustar un modelo es sumamente costoso computacionalmente.

Para escenarios como el de este curso, donde los datos no abundan, utilzaremos un partición de train/test junto a validación cruzada. La idea es la siguiente:

Dividir de conjunto de datos en train y test.
Definir posibles modelos.
Ajustar los mejores hiperparámetros utilizando validación cruzada en el conjunto de entrenamiento.
Declarar el error/score del modelo utilizando la partición de test.

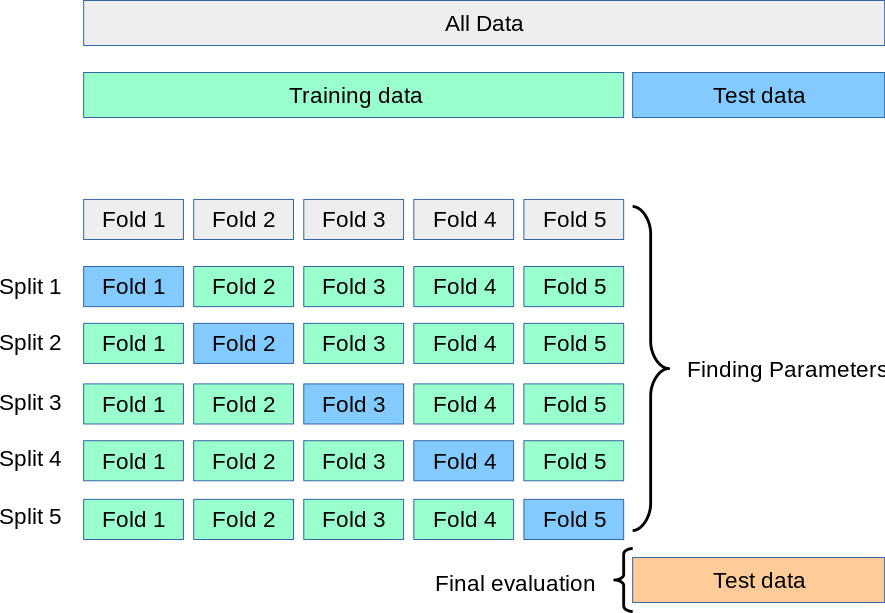
select_model

Consideremos otro modelo de regresión para los datos ya trabajados. La regresión Lasso es similar a Ridge pero la regularización es respecto a una norma \(l_1\).

\[ \min_\beta \frac{1}{2 n_{samples}} \vert \vert y - X \beta \vert \vert_2^2 + \alpha \vert \vert \beta \vert \vert_1^2 \]

from sklearn.linear_model import Lasso

est_lasso = Lasso(alpha=0.1)

est_lasso.fit(X_train, y_train)
est_lasso.score(X_test, y_test)

0.666045437403698

Partición train/test¶

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

Posibles Modelos¶

Pensemos en escoger entre una regresión Ridge y una Lasso.

ridge = Ridge()
lasso = Lasso()

Hyperparameters Tuning¶

En este caso cada uno tiene un solo parámetros a ajustar y coincidemente se llaman iguales, pero no siempre es el caso.

ridge_grid = {"alpha": np.arange(0.1, 10, 0.05)}

ridge_cv = GridSearchCV(
    estimator=ridge,
    param_grid=ridge_grid
)

ridge_cv.fit(X_train, y_train)
ridge_cv.best_params_

{'alpha': 0.1}

lasso_grid = {"alpha": np.arange(0.1, 10, 0.05)}

lasso_cv = GridSearchCV(
    estimator=lasso,
    param_grid=lasso_grid
)

lasso_cv.fit(X_train, y_train)
lasso_cv.best_params_

{'alpha': 0.1}

Obtener scores¶

ridge_cv.score(X_test, y_test)

0.6838049959091362

lasso_cv.score(X_test, y_test)

0.666045437403698

ridge_cv.score(X_test, y_test) > lasso_cv.score(X_test, y_test)

True

Como el error de predicción en el modelo de regresión Ridge es mejor nos quedamos con él como el modelo ganador.

MAT281 - Aplicaciones de la Matemática en la Ingeniería - 2020

Selección de Modelos¶

Estimadores¶

Pre-Procesamiento¶

Pipelines¶

Evaluación de Modelos¶

Búsqueda de Hiper-parámetros¶

Selección de Modelos¶

Partición train/test¶

Posibles Modelos¶

Hyperparameters Tuning¶

Obtener scores¶