.ipynb .pdf

repository

Binder Colab

Contents

Clustering

Aprendizaje No Supervisado

En las últimas clases hemos aprendido técnicas de Machine Learning que pertenecen al Aprendizaje Supervisado, pues los datos vienen clasificados previamente, ya sea en un Regresión que se posee el valor cuantitativo, como en Clasificación donde se posee la etiqueta del registro. Con esto el algoritmo produce una función que establece una correspondencia entre las entradas y las salidas deseadas del sistema.

Mientras que el Aprendizaje No Supervisado difiere del anterior en que los datos no vienen clasificados previamente. Aquí el sistema tiene que ser capaz de reconocer patrones para poder etiquetar las nuevas entradas. Es importante tener en consideración que estas etiquetas son artificiales, puede que no tengan ninguna interpretación!

Clustering

En palabras simples: agrupar registros sin etiqueta previa. Se refiere a una serie de técnicas para encontrar subgrupos o clusters en un conjunto de datos. Los elementos de cada uno de estos subgrupos son “similares” unos de otros. Es importante entonces definir esta medida de similaridad.

Motivación

Buscaremos ilustrar los distintos algoritmos con datos reales. Un conjunto de datos interesante y versatil es el Iris Dataset.

Recuerdo: El conjunto de datos consiste en 50 muestras de 3 especies de Iris (Iris setosa, Iris virginica y Iris versicolor). Para cada flor, se midieron 4 características: largo y ancho de los petalos, y largo y ancho de los sépalos, en centímetros.

import altair as alt
from vega_datasets import data

alt.themes.enable('opaque')  # Para quienes utilizan temas oscuros en Jupyter Lab/Notebook

ThemeRegistry.enable('opaque')

iris_df = data.iris()
iris_df.head()

	sepalLength	sepalWidth	petalLength	petalWidth	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

alt.Chart(iris_df).mark_circle(opacity=0.5).encode(
    alt.X(alt.repeat("column"), type='quantitative'),
    alt.Y(alt.repeat("row"), type='quantitative'),
    color='species:N'
).properties(
    width=150,
    height=150
).repeat(
    row=['petalLength', 'petalWidth', 'sepalLength', 'sepalWidth'],
    column=['sepalWidth', 'sepalLength', 'petalWidth', 'petalLength']
)

Pregunta de vital importancia para el desarrollo de la trama: ¿Si no supiéramos que existen 3 tipos de Iris, seríamos capaces algorítmicamente de encontrar 3 tipos de flores?

alt.Chart(iris_df).mark_circle(opacity=0.5).encode(
    alt.X(alt.repeat("column"), type='quantitative'),
    alt.Y(alt.repeat("row"), type='quantitative'),
).properties(
    width=150,
    height=150
).repeat(
    row=['petalLength', 'petalWidth', 'sepalLength', 'sepalWidth'],
    column=['sepalWidth', 'sepalLength', 'petalWidth', 'petalLength']
)

Para determinar que nos encontramos frente a un problema que necesita de un algoritmo de Clustering:

• Se tienen datos sin etiquetar/agrupar.

• Se busca obtener un agrupamiento “natural” de los datos.

• No existen ejemplos de los cuales aprender: método sin supervisar.

• Fácil de verificar por inspección visual en 2D y 3D.

• Difícil de verificar en dimensiones superiores.

Algunos ejemplos de aplicaciones

• Segmentación de mercado:

  • ¿Cómo atendemos mejor a nuestros clientes?

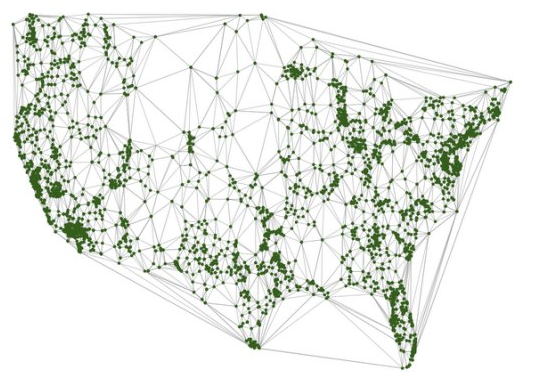
• Ubicación de centros de reabastacimiento:

  • ¿Cómo minimizamos tiempos de entrega?

• Compresión de imágenes:

  • ¿Cómo minimizamos el espacio destinado al almacenamiento?

1. Ubicación centros de reabastecimiento

1. Compresión de Imágenes

   • Utilizando todos los colores:

   

   • Utilizando únicamente 32 colores:

   

2. ** Segmentación de mercados **

Características de un Problema de Clustering

• Datos de entrada: Conjunto de inputs sin etiquetas.

• Datos de salida: Etiquetas para cada input.

Observación: La etiqueta/label típicamente se asocia a un entero (0,1,2, etc.) pero en realidad es cualquier variable categórica.

Algoritmos de Clustering

Buscan utilizar las propiedades inherentes presentes en los datos para organizarlos en grupos de máxima similitud.

• Algoritmos basados en conectividad: Hierarchical Clustering.

• Algoritmos basados en densidad: Expectation Maximization

• Algoritmos basados en centroides: k-means.

k-means

• Input: set \(X\) de \(N\) datos \(x=(x_1, ..., x_n)\) y un hiper-parámetro \(k\) con el número de clusters a crear.

• Output: Set de \(k\) centroides de clusters (\(\mu_l\)) y una etiquetación de cada dato \(x\) en \(X\) indicando a qué cluster pertenece.

\(x_i\) y \(\mu_l\) son vectores en \(\mathcal{R}^m\).

La pertenencia es única. Todos los puntos dentro de un cluster se encuentran mas cercanos en distancia al centroide de su cluster que al centroide de otro cluster.

Matemáticamente:

\begin{align*} \textrm{Minimizar } \sum_{l=1}^k \sum_{x_n \in C_l} ||x_n - \mu_l ||^2 \textrm{ respecto a } C_l, \mu_l. \end{align*}

Donde \(C_l\) es el cluster l-ésimo.

El problema anterior es NP-hard (imposible de resolver en tiempo polinomial, del tipo más difícil de los probleams NP).

Algoritmo de Lloyd

Heurística que converge en pocos pasos a un mínimo local.

Procedimiento

• Calcular el centroide del cluster promediando las posiciones de los puntos actualmente en el cluster.

• Actualizar la pertenencia a los clusters utilizando la distancia más cercana a cada centroide.

En este caso, un video vale más que mil palabras

from IPython.display import YouTubeVideo
display(YouTubeVideo("5I3Ei69I40s"))

¿Cuándo funciona k-means?

Cuando los clusters son bien definidos y pueden separarse por círculos (n-esferas) de igual tamaño.

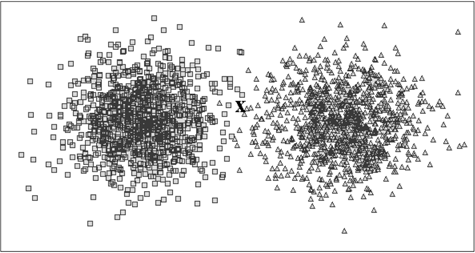
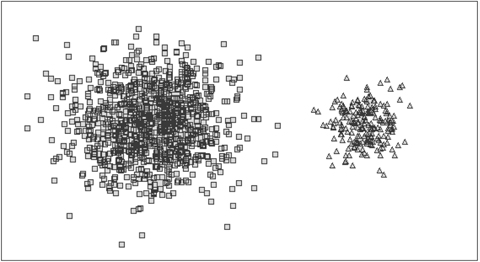
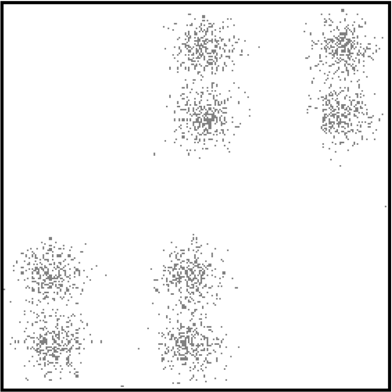
¿Cuándo falla k-means?

• Cuando se selecciona mal el número \(k\) de clusters.

• Cuando no existe separación clara entre los clusters.

• Cuando los clusters son de tamaños muy distintos.

• Cuando la inicialización no es apropiada.

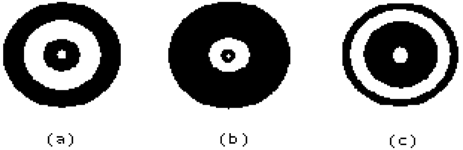
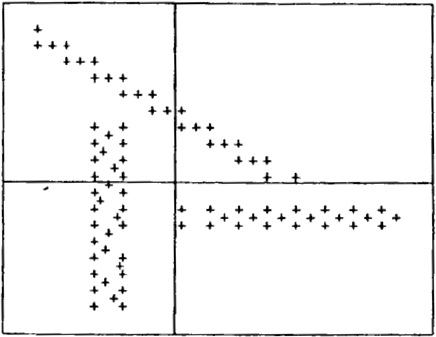
Ventajas

• Rápido y sencillo de programar

Desventajas

• Trabaja en datos continuos, o donde distancias y promedios pueden definirse.

• Heurística depende del puntos iniciales.

• Requiere especificar el número de clusters \(k\).

• No funciona correctamente en todos los casos de clustering, incluso conociendo \(k\) correctamente.

Implementación

import numpy as np
import pandas as pd

from scipy.linalg import norm
from sklearn.datasets import make_blobs

def find_centers(X, k, seed=None):
    if seed is None:
        seed = 42
    np.random.seed(seed)
    # Initialize to K random centers
    old_centroids = random_centers(X, k)
    new_centroids = random_centers(X, k)
    while not has_converged(new_centroids, old_centroids):
        old_centroids = new_centroids
        # Assign all points in X to clusters
        clusters = cluster_points(X, old_centroids)
        # Reevaluate centers
        new_centroids = reevaluate_centers(X, clusters, k)
    return (new_centroids, clusters)


def random_centers(X, k):
    index = np.random.randint(0, X.shape[0], k)
    return X[index, :]


def has_converged(new_mu, old_mu, tol=1E-6):
    num = norm(np.array(new_mu)-np.array(old_mu))
    den = norm(new_mu)
    rel_error= num/den
    return rel_error < tol


def cluster_points(X, centroids):
    clusters = []
    for i, x in enumerate(X):
        distances = np.array([norm(x-cj) for cj in centroids])
        clusters.append( distances.argmin())
    return np.array(clusters)


def reevaluate_centers(X, clusters, k):
    centroids = []
    for j in range(k):
        cj = X[clusters==j,:].mean(axis=0)
        centroids.append(cj)
    return centroids

Ejemplo con datos sintéticos

N = 1000
k = 4

X, y = make_blobs(
    n_samples=N,
    centers=k,
    random_state=42,
    cluster_std=0.60
)

blobs = pd.DataFrame(X, columns=["x", "y"])
alt.Chart(blobs).mark_circle().encode(
    x="x",
    y="y"
).properties(
    width=600,
    height=400
)

Probando la implementación

centroids, clusters = find_centers(X, k=4, seed=42)

blobs["cluster"] = clusters
centroids_df = pd.DataFrame(centroids, columns=["x", "y"])

blobs_points = alt.Chart(blobs).mark_circle().encode(
    x="x",
    y="y",
    color="cluster:N"
).properties(
    width=600,
    height=400
)

blobs_centroids = alt.Chart(centroids_df).mark_point(size=250, fill="black", filled=True, fillOpacity=1, shape="cross").encode(
    x="x",
    y="y",
).properties(
    width=600,
    height=400
)

blobs_points + blobs_centroids

Implementación de scikit-learn

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
centroids = kmeans.cluster_centers_
clusters = kmeans.labels_
blobs["cluster"] = clusters
centroids_df = pd.DataFrame(centroids, columns=["x", "y"])

blobs_points = alt.Chart(blobs).mark_circle().encode(
    x="x",
    y="y",
    color="cluster:N"
).properties(
    width=600,
    height=400
)

blobs_centroids = alt.Chart(centroids_df).mark_point(size=250, fill="black", filled=True, fillOpacity=1, shape="cross").encode(
    x="x",
    y="y",
).properties(
    width=600,
    height=400
)

blobs_points + blobs_centroids

Comparación

N = 100000
k = 6

X, y = make_blobs(
    n_samples=N,
    centers=k,
    random_state=42,
    cluster_std=0.60
)

%%timeit
centroids, clusters = find_centers(X, k=4, seed=42)

%%timeit
kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
centroids = kmeans.cluster_centers_
clusters = kmeans.labels_

1.22 s ± 328 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

No es sorprendente la verdad… No es necesario volver a inventar la rueda, pero si saber como funciona.

Ejemplo Iris Dataset

Vamos a abusar un poco de este conjunto, pues ya conocemos su clasificación, pero es un buen ejemplo para probar un algoritmo de Clustering.

from sklearn import datasets
from sklearn.metrics import confusion_matrix

# Parameters
n_clusters = 3

# Loading the data
iris = datasets.load_iris()
X_iris = iris.data
y_iris_true = iris.target

# Running the algorithm
kmeans = KMeans(n_clusters)
kmeans.fit(X_iris)
y_pred = kmeans.labels_

# Show the classificacion report
cm = confusion_matrix(y_iris_true, y_pred)
print(cm)
print(f"\nAccuracy: {(np.diag(cm).sum() ) / float(cm.sum())}") # 16/100

[[50  0  0]
 [ 0 48  2]
 [ 0 14 36]]

Accuracy: 0.8933333333333333

¿Hay algo que te parece raro en esta matriz de confusión?

Ejemplo Compresión de Imágenes

from pathlib import Path
from PIL import Image

# Load image
im_filepath = Path().resolve().parent / "images" / "coyoya.jpg"
im = Image.open(im_filepath)
im

k = 8  # Number of clusters
X = np.array(im.getdata())  # Array with image values
kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
compressed_array = kmeans.cluster_centers_[kmeans.predict(X)]  # Prediction 
im_compressed = compressed_array.astype(np.uint8).reshape(im.size[1], im.size[0], 3)  # New image
Image.fromarray(im_compressed, mode="RGB")

Clasificación II Cross-Validation