Introducción al Cálculo Científico¶
En esta clase introduciremos algunos conceptos de computación cientifica en Python, principalmente utilizando la biblioteca NumPy, piedra angular de otras librerías científicas.
SciPy.org¶
SciPy es un ecosistema de software open-source para matemática, ciencia y engeniería. Las principales bibliotecas son:
NumPy: Arrays N-dimensionales. Librería base, integración con C/C++ y Fortran.
SciPy library: Computación científica (integración, optimización, estadística, etc.)
Matplotlib: Visualización 2D:
IPython: Interactividad (Project Jupyter).
SimPy: Matemática Simbólica.
Pandas: Estructura y análisis de datos.
Numpy¶
NumPy es el paquete fundamental para la computación científica en Python. Proporciona un objeto de matriz multidimensional, varios objetos derivados (como matrices y arreglos) y una variedad de rutinas para operaciones rápidas en matrices, incluida la manipulación matemática, lógica, de formas, clasificación, selección, I/O, transformadas discretas de Fourier, álgebra lineal básica, operaciones estadísticas básicas, simulación y mucho más. Fuente.
Para comenzar, la forma usual de importar NumPy es utilizando el alias np. Lo verás así en una infinidad de ejmplos, libros, blogs, etc.
import numpy as np
Lo básico¶
Los objetos principales de Numpy son los comúnmente conocidos como NumPy Arrays (la clase se llama ndarray), corresponden a una tabla de elementos, todos del mismo tipo, indexados por una tupla de enternos no-negativos. En NumPy, las dimensiones son llamadas axes (ejes) y su singular axis (eje), similar a un plano cartesiano generalizado. Esta parte de la clase está basada en el Quickstart tutorial en la página oficial (link).
Instanciar un NumPy Array es simple es utilizando el constructor propio de la biblioteca.
a = np.array(
[
[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]
]
)
type(a)
numpy.ndarray
Los atributos más importantes de un ndarray son:
a.shape # the dimensions of the array.
(3, 5)
a.ndim # the number of axes (dimensions) of the array.
2
a.size # the total number of elements of the array.
15
a.dtype # an object describing the type of the elements in the array.
dtype('int64')
a.itemsize # the size in bytes of each element of the array.
8
Crear Numpy Arrays¶
Hay varias formas de crear arrays, el constructor básico es el que se utilizó hace unos momentos, np.array. El type del array resultante es inferido de los datos proporcionados.
a_int = np.array([2, 6, 10])
a_float = np.array([2.1, 6.1, 10.1])
print(f"a_int: {a_int.dtype.name}")
print(f"a_float: {a_float.dtype.name}")
a_int: int64
a_float: float64
También es posible utilizar otras estructuras de Python, como listas o tuplas.
a_list = [1, 1, 2, 3, 5]
np.array(a_list)
array([1, 1, 2, 3, 5])
a_tuple = (1, 1, 1, 3, 5, 9)
np.array(a_tuple)
array([1, 1, 1, 3, 5, 9])
¡Cuidado! Es fácil confundirse con las dimensiones o el tipo de argumento en los contructores de NumPy, por ejemplo, utilizando una lista podríamos crear un arreglo de una o dos dimensiones si no tenemos cuidado.
one_dim_array = np.array(a_list)
two_dim_array = np.array([a_list])
print(f"np.array(a_list) = {one_dim_array} tiene shape: {one_dim_array.shape}, es decir, {one_dim_array.ndim} dimensión(es).")
print(f"np.array([a_list]) = {two_dim_array} tiene shape: {two_dim_array.shape}, es decir, {two_dim_array.ndim} dimensión(es).")
np.array(a_list) = [1 1 2 3 5] tiene shape: (5,), es decir, 1 dimensión(es).
np.array([a_list]) = [[1 1 2 3 5]] tiene shape: (1, 5), es decir, 2 dimensión(es).
Una funcionalidad útil son los constructores especiales a partir de constantes.
np.zeros((3, 4))
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
np.ones((2, 3, 4), dtype=np.int) # dtype can also be specified
array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]])
np.identity(4) # Identity matrix
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
Por otro lado, NumPy proporciona una función análoga a range.
range(10)
range(0, 10)
type(range(10))
range
np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
type(np.arange(10))
numpy.ndarray
np.arange(3, 10)
array([3, 4, 5, 6, 7, 8, 9])
np.arange(2, 20, 3, dtype=np.float)
array([ 2., 5., 8., 11., 14., 17.])
np.arange(9).reshape(3, 3)
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
Bonus: Utilizar np.arange tiene como “ingredientes” el inicio (start), fin (stop) y el tamaño del espacio entre valores (step) y el largo (len) depende estos argumentos. Sin embargo, existe la función np.linspace que construye un np.array con un inicio y un fin, pero indicando la cantidad de elementos (y por lo tanto, el espaciado depende es este).
np.linspace(0, 100, 5)
array([ 0., 25., 50., 75., 100.])
Esto puede causar confusiones en ocasiones, pues recuerda que la indexación de Python (y por lo tanto NumPy) comienza en cero, por lo que si quieres replicar el np.array anterior con np.arange debes tener esto en consideración. Es decir:
np.arange(start=0, stop=100, step=25) # stop = 100
array([ 0, 25, 50, 75])
np.arange(start=0, stop=101, step=25) # stop = 101
array([ 0, 25, 50, 75, 100])
No podía faltar la instanciación a través de elementos aleatorios
np.random.random(size=3) # Elementos entre 0 y 1
array([0.96165579, 0.77606847, 0.45565248])
np.random.uniform(low=3, high=7, size=5) # Desde una distribución uniforme
array([5.43713347, 6.38887844, 3.08124221, 5.89289897, 4.22273772])
np.random.normal(loc=100, scale=10, size=(2, 3)) # Desde una distribución normal indicando media y desviación estándar
array([[104.60216161, 100.60921685, 107.82969819],
[ 93.05321527, 103.01779242, 98.19886912]])
Acceder a los elementos de un array¶
Es muy probable que necesites acceder a elementos o porciones de un array, para ello NumPy tiene una sintáxis consistente con Python.
x1 = np.arange(0, 30, 4)
x2 = np.arange(0, 60, 3).reshape(4, 5)
print("x1:")
print(x1)
print("\nx2:")
print(x2)
x1:
[ 0 4 8 12 16 20 24 28]
x2:
[[ 0 3 6 9 12]
[15 18 21 24 27]
[30 33 36 39 42]
[45 48 51 54 57]]
x1[1] # Un elemento de un array 1D
4
x1[:3] # Los tres primeros elementos
array([0, 4, 8])
x2[0, 2] # Un elemento de un array 2D
6
x2[0] # La primera fila
array([ 0, 3, 6, 9, 12])
x2[:, 1] # Todas las filas y la segunda columna
array([ 3, 18, 33, 48])
x2[:, 1:3] # Todas las filas y de la segunda a la tercera columna
array([[ 3, 6],
[18, 21],
[33, 36],
[48, 51]])
Nuevamente, recordar que Python tiene indexación partiendo desde cero. Además, la dimensión del arreglo también depende de la forma en que se haga la selección.
x2[:, 2]
array([ 6, 21, 36, 51])
x2[:, 2:3] # What?!
array([[ 6],
[21],
[36],
[51]])
En el ejemplo anterior los valores son los mismos, pero las dimensiones no. En el primero se utiliza indexing para acceder a la tercera columna, mientras que en el segundo slicing para acceder desde la tercera columna a la tercera columna.
print(x2[:, 2].shape)
print(x2[:, 2:3].shape)
(4,)
(4, 1)
Operaciones Básias¶
Numpy provee operaciones vectorizadas, con tal de mejorar el rendimiento de la ejecución.
Por ejemplo, pensemos en la suma de dos arreglos 2D.
A = np.random.random((5,5))
B = np.random.random((5,5))
Con los conocimientos de la clase pasada, podríamos pensar en iterar a través de dos for, con tal de llenar el arreglo resultando. algo así:
def my_sum(A, B):
n, m = A.shape
C = np.empty(shape=(n, m))
for i in range(n):
for j in range(m):
C[i, j] = A[i, j] + B[i, j]
return C
%timeit my_sum(A, B)
16.2 µs ± 297 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Pero la suma de ndarrays es simplemente con el signo de suma (+):
%timeit A + B
537 ns ± 0.869 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
Para dos arrays tan pequeños la diferencia de tiempo es considerable, ¡Imagina con millones de datos!
Los clásicos de clásicos:
x = np.arange(5)
print(f"x = {x}")
print(f"x + 5 = {x + 5}")
print(f"x - 5 = {x - 5}")
print(f"x * 2 = {x * 2}")
print(f"x / 2 = {x / 2}")
print(f"x // 2 = {x // 2}")
print(f"x ** 2 = {x ** 2}")
print(f"x % 2 = {x % 2}")
x = [0 1 2 3 4]
x + 5 = [5 6 7 8 9]
x - 5 = [-5 -4 -3 -2 -1]
x * 2 = [0 2 4 6 8]
x / 2 = [0. 0.5 1. 1.5 2. ]
x // 2 = [0 0 1 1 2]
x ** 2 = [ 0 1 4 9 16]
x % 2 = [0 1 0 1 0]
¡Júntalos como quieras!
-(0.5 + x + 3) ** 2
array([-12.25, -20.25, -30.25, -42.25, -56.25])
Al final del día, estos son alias para funciones de Numpy, por ejemplo, la operación suma (+) es un wrapper de la función np.add
np.add(x, 5)
array([5, 6, 7, 8, 9])
Podríamos estar todo el día hablando de operaciones, pero básicamente, si piensas en alguna operación lo suficientemente común, es que la puedes encontrar implementada en Numpy. Por ejemplo:
np.abs(-(0.5 + x + 3) ** 2)
array([12.25, 20.25, 30.25, 42.25, 56.25])
np.log(x + 5)
array([1.60943791, 1.79175947, 1.94591015, 2.07944154, 2.19722458])
np.exp(x)
array([ 1. , 2.71828183, 7.3890561 , 20.08553692, 54.59815003])
np.sin(x)
array([ 0. , 0.84147098, 0.90929743, 0.14112001, -0.7568025 ])
Para dimensiones mayores la idea es la misma, pero siempre hay que tener cuidado con las dimensiones y shape de los arrays.
print("A + B: \n")
print(A + B)
print("\n" + "-" * 80 + "\n")
print("A - B: \n")
print(A - B)
print("\n" + "-" * 80 + "\n")
print("A * B: \n")
print(A * B) # Producto elemento a elemento
print("\n" + "-" * 80 + "\n")
print("A / B: \n")
print(A / B) # División elemento a elemento
print("\n" + "-" * 80 + "\n")
print("A @ B: \n")
print(A @ B) # Producto matricial
A + B:
[[0.36641902 1.10265758 0.97080253 1.61427266 1.10848218]
[0.6980639 1.02215826 0.33492285 1.09431768 1.16570131]
[0.58299357 1.22340948 0.62221823 0.75374863 0.91516117]
[1.62053995 0.85742391 1.77298672 1.01488167 0.64104018]
[1.23877663 1.52619614 1.70190349 1.12218395 1.41613267]]
--------------------------------------------------------------------------------
A - B:
[[-0.08307907 -0.16907341 0.59270808 -0.13320033 0.15083695]
[-0.07945091 0.7505947 -0.1826062 -0.316115 0.61827474]
[ 0.38407445 0.35219947 -0.43638885 0.4595377 -0.73772994]
[-0.03996857 0.44160434 0.18059724 0.79528976 0.33486536]
[ 0.0267252 0.08823926 0.12273678 0.72022703 0.56097398]]
--------------------------------------------------------------------------------
A * B:
[[0.03184019 0.29681698 0.14778867 0.64703348 0.30149524]
[0.12024519 0.12035377 0.01970707 0.27440062 0.24414898]
[0.04809208 0.34317157 0.04918007 0.08924052 0.07331863]
[0.65613806 0.13504034 0.77771664 0.09937475 0.07469943]
[0.38346333 0.58037212 0.72035279 0.18514246 0.42268498]]
--------------------------------------------------------------------------------
A / B:
[[0.6303474 0.73410507 4.13523812 0.84755092 1.31501635]
[0.79562857 6.52794872 0.29431517 0.55174748 3.25884078]
[4.86161407 1.80852946 0.17554141 4.12386558 0.10734599]
[0.95185984 3.12401907 1.22682547 8.24334324 3.18741275]
[1.04409911 1.12272865 1.155445 4.5836031 2.31197632]]
--------------------------------------------------------------------------------
A @ B:
[[1.28748531 1.10067779 1.64813712 0.77582799 1.22427637]
[1.28529716 1.07242418 1.34224653 1.12853499 0.89461885]
[0.9816119 0.64481785 0.89750116 1.07615905 0.6547509 ]
[1.57443388 1.55520675 1.94039586 1.48968361 1.71064846]
[1.9106845 1.8116373 2.32539761 1.55615051 1.84161453]]
Operaciones Booleanas¶
print(f"x = {x}")
print(f"x > 2 = {x > 2}")
print(f"x == 2 = {x == 2}")
print(f"x == 2 = {x == 2}")
x = [0 1 2 3 4]
x > 2 = [False False False True True]
x == 2 = [False False True False False]
x == 2 = [False False True False False]
aux1 = np.array([[1, 2, 3], [2, 3, 5], [1, 9, 6]])
aux2 = np.array([[1, 2, 3], [3, 5, 5], [0, 8, 5]])
B1 = aux1 == aux2
B2 = aux1 > aux2
print("B1: \n")
print(B1)
print("\n" + "-" * 80 + "\n")
print("B2: \n")
print(B2)
print("\n" + "-" * 80 + "\n")
print("~B1: \n")
print(~B1) # También puede ser np.logical_not(B1)
print("\n" + "-" * 80 + "\n")
print("B1 | B2 : \n")
print(B1 | B2)
print("\n" + "-" * 80 + "\n")
print("B1 & B2 : \n")
print(B1 & B2)
B1:
[[ True True True]
[False False True]
[False False False]]
--------------------------------------------------------------------------------
B2:
[[False False False]
[False False False]
[ True True True]]
--------------------------------------------------------------------------------
~B1:
[[False False False]
[ True True False]
[ True True True]]
--------------------------------------------------------------------------------
B1 | B2 :
[[ True True True]
[False False True]
[ True True True]]
--------------------------------------------------------------------------------
B1 & B2 :
[[False False False]
[False False False]
[False False False]]
Broadcasting¶
¿Qué pasa si las dimensiones no coinciden? Observemos lo siguiente:
a = np.array([0, 1, 2])
b = np.array([5, 5, 5])
a + b
array([5, 6, 7])
Todo bien, dos arrays 1D de 3 elementos, la suma retorna un array de 3 elementos.
a + 3
array([3, 4, 5])
Sigue pareciendo normal, un array 1D de 3 elementos, se suma con un int, lo que retorna un array 1D de tres elementos.
M = np.ones((3, 3))
M
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
M + a
array([[1., 2., 3.],
[1., 2., 3.],
[1., 2., 3.]])
Magia! Esto es broadcasting. Una pequeña infografía para digerirlo:
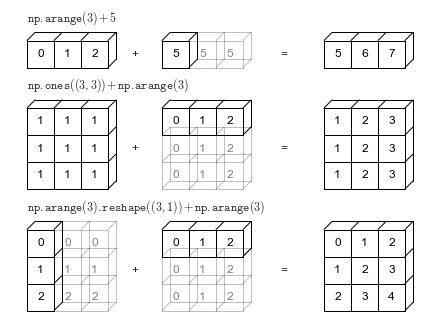
Resumen: A lo menos los dos arrays deben coincidir en una dimensión. Luego, el array de dimensión menor se extiende con tal de ajustarse a las dimensiones del otro.
La documentación oficial de estas reglas la puedes encontrar aquí.
