Visualización Imperativa¶
Los objetivos de esta clase son:
Comprender el estilo de visualización imperativa.
Aplicar gráficos adecuados dependiendo de los datos.
Gráficos con Matplotlib
El paradigma de la visualización imperativa se focaliza en las instrucciones recibidas, ya que no abstrae las operaciones o codificaciones visuales. Algunas de sus características son:
Se especifica cómo se debe hacer algo.
Se deben especificar manualmente los pasos del trazado.
Especificación y ejecución entrelazadas.
Coloquialmente se puede entender como que se debe decidir pixel a pixel lo que se desea mostrar.
Matplotlib¶
Lo mejor para entender una librería es la explicación que entrega la misma comunidad, a continuación un extracto de la página web de matplotlib:
Matplotlib is a Python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms. Matplotlib can be used in Python scripts, the Python and IPython shells, the Jupyter notebook, web application servers, and four graphical user interface toolkits.
Matplotlib tries to make easy things easy and hard things possible. You can generate plots, histograms, power spectra, bar charts, errorcharts, scatterplots, etc., with just a few lines of code. For examples, see the sample plots and thumbnail gallery.
For simple plotting the pyplot module provides a MATLAB-like interface, particularly when combined with IPython. For the power user, you have full control of line styles, font properties, axes properties, etc, via an object oriented interface or via a set of functions familiar to MATLAB users.
Conceptos Generales¶
El trazado requiere acción en un rango de niveles, desde el más general (por ejemplo, ‘contornear este arreglo 2D’) hasta el más específico (por ejemplo, ‘colorear un píxel de color rojo’). El propósito de esta librería es generar gráficos de manera rápida lo más fácil posible (con código de alto nivel), pero con la capacidad de usar código de bajo nivel cuando sea necesario.
Por lo tanto, todo en matplotlib está organizado en una jerarquía. En la parte superior se encuentra el módulo matplotlib.pyplot. En este nivel, se utilizan funciones simples para agregar elementos de trazado (líneas, imágenes, texto, etc.) a los ejes actuales en la figura actual. El siguiente nivel en la jerarquía es el primer nivel de la interfaz orientada a objetos, en la que pyplot se usa solo para algunas funciones, como la creación de figuras, y el usuario crea y realiza un seguimiento explícito de los objetos de figuras y ejes. En este nivel, el usuario usa pyplot para crear figuras, y a través de esas figuras, se pueden crear uno o más objetos de ejes. Estos objetos de ejes se utilizan para la mayoría de las acciones de trazado.
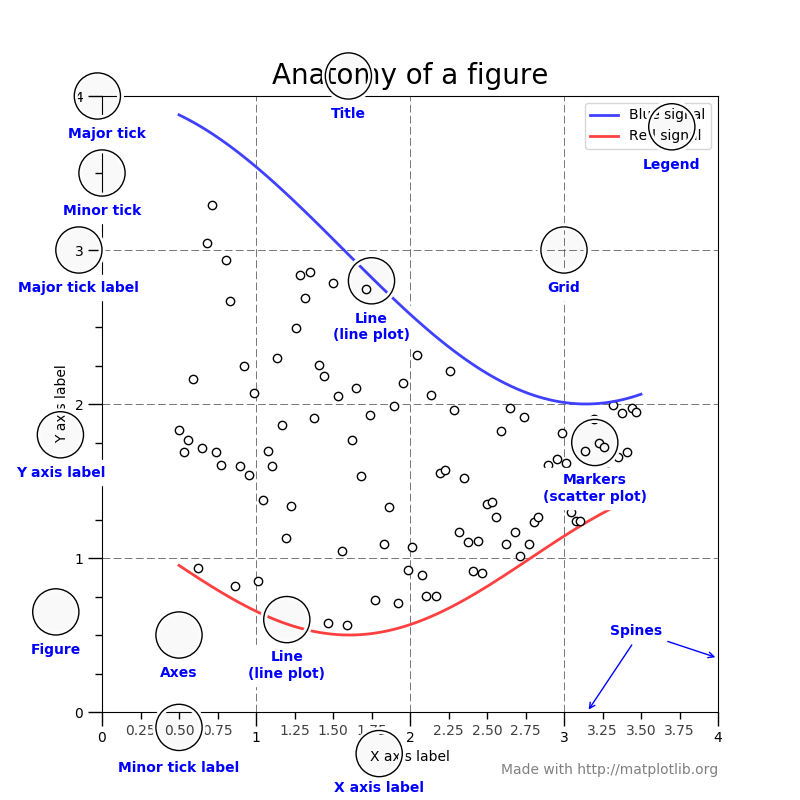
Figure¶
Es la visualización completa. Figure realiza un seguimiento de todos los Axes hijos y el Canvas. Una figura puede tener cualquier número de Axes, pero para ser útil debe tener al menos uno.
La forma más fácil de crear una nueva Figure es con pyplot:
fig = plt.figure() # an empty figure with no axes
fig, ax_lst = plt.subplots(2, 2) # a figure with a 2x2 grid of Axes
Axes¶
Esto es lo que se puede pensar como ‘un gráfico’, es la región de la imagen con el espacio de datos. Un Figure dada puede contener muchos Axes, pero un objeto Axe dado solo puede estar en un Figure. Axes contiene dos (o tres en el caso de 3D) objetos Axis que se ocupan de los límites de datos. Cada Axe tiene un título, una etiqueta para el eje horizonal y una etiqueta para el eje vertical.
La clase Axes y sus funciones son el punto de entrada principal para trabajar con la interfaz orientada a objetos.
Axis¶
Corresponden a los ejes, algo así como líneas rectas. Se encargan de establecer los límites del gráfico y generar los ticks (las marcas en el eje) y los ticklabels (strings que etiquetan los ticks).
Gráfico a Gráfico¶
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.stats import multivariate_normal
%matplotlib inline
Gráfico de Barras¶
people = ('Tom', 'Dick', 'Harry', 'Slim', 'Jim')
y_pos = np.arange(len(people))
performance = 3 + 10 * np.random.rand(len(people))
error = np.random.rand(len(people))
# Another way without axes
fig = plt.figure(figsize=(20, 10))
plt.subplot(1, 2, 1)
plt.barh(y_pos, performance, xerr=error, align='center', color="g", alpha=0.4)
plt.yticks(y_pos, people)
plt.xlabel('Performance')
plt.subplot(1, 2, 2)
plt.bar(y_pos, performance, yerr=error, align='center', color="g", alpha=0.6)
plt.xticks(y_pos, people)
plt.xlabel('People')
plt.ylabel('Performance')
plt.show()
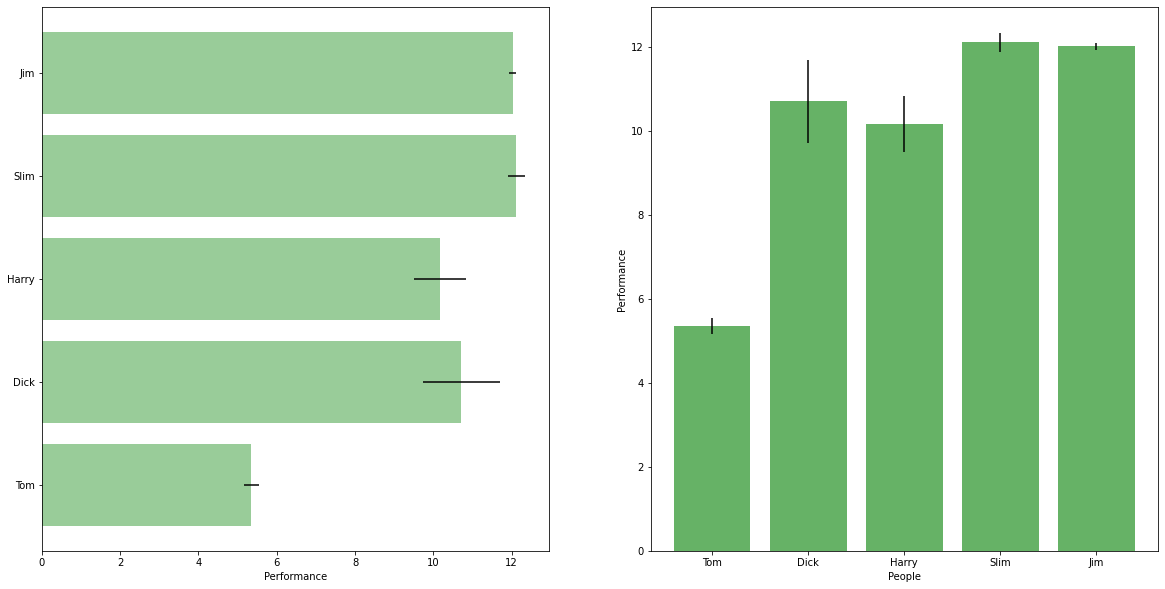
¿Cuándo utilizar gráfico de barras?
x: Debe ser datos del tipo nominal o ordinal.
y: Debe ser datos de tipo ordinal, posicional o cuantitativo.
Evitar a toda costa gráfico de nominal vs nominal.
Gráfico de Líneas¶
def f(t):
return np.exp(-t) * np.cos(2 * np.pi * t)
t1 = np.arange(0.0, 5.0, 0.5)
t2 = np.arange(0.0, 5.0, 0.02)
fig, (ax1, ax2) = plt.subplots(nrows=2, figsize=(20, 10), sharex=True, sharey=True)
ax1.plot(t1, f(t1), marker='o')
ax1.grid()
ax1.set_title("arange step = 0.5")
ax2.plot(t2, f(t2))
ax2.grid()
ax2.set_title("arange step = 0.02")
fig.show()
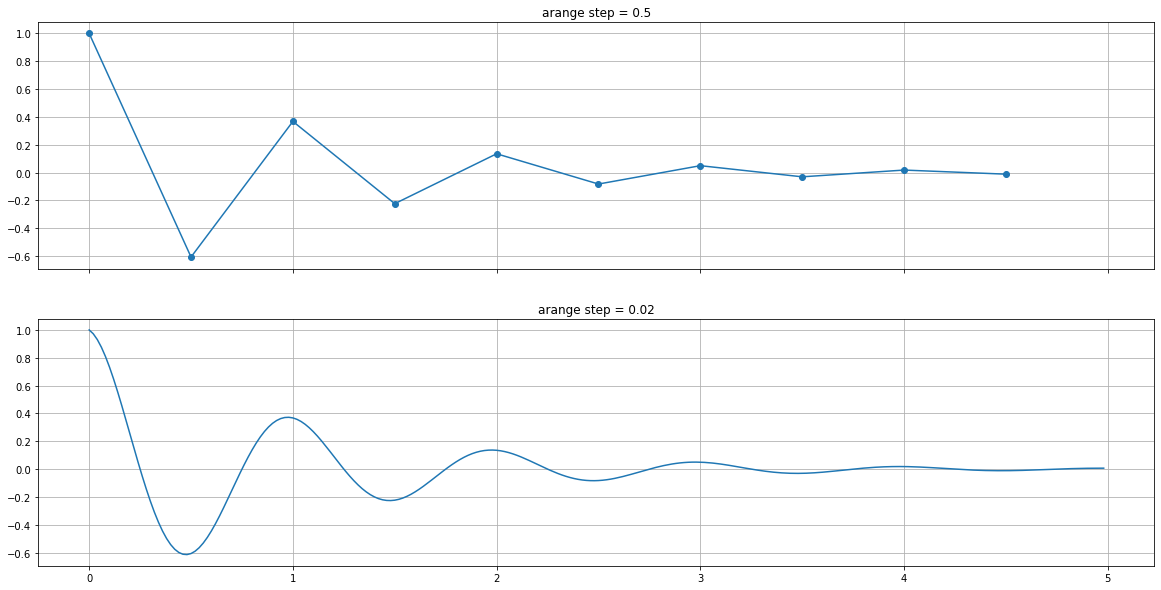
¿Cuándo utilizar gráfico de líneas?
x: Debe ser datos del tipo ordinal o cuantitativo.
y: Debe ser datos de tipo ordinal, posicional o cuantitativo.
Gráfico de Barra de Error¶
Literalmente una gráfico de líneas pero útil cuando en ciertos puntos es necesario agregar algún intervalo, típicamente de error.
x = np.arange(0.1, 4, 0.5)
y = np.exp(-x)
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(20, 10))
x_error = 0.1 + 0.2 * np.random.rand(len(x))
ax1.errorbar(x, y, xerr=x_error)
y_error = 0.1 + 0.2 * np.random.rand(len(x))
ax2.errorbar(x, y, yerr=y_error)
fig.show()
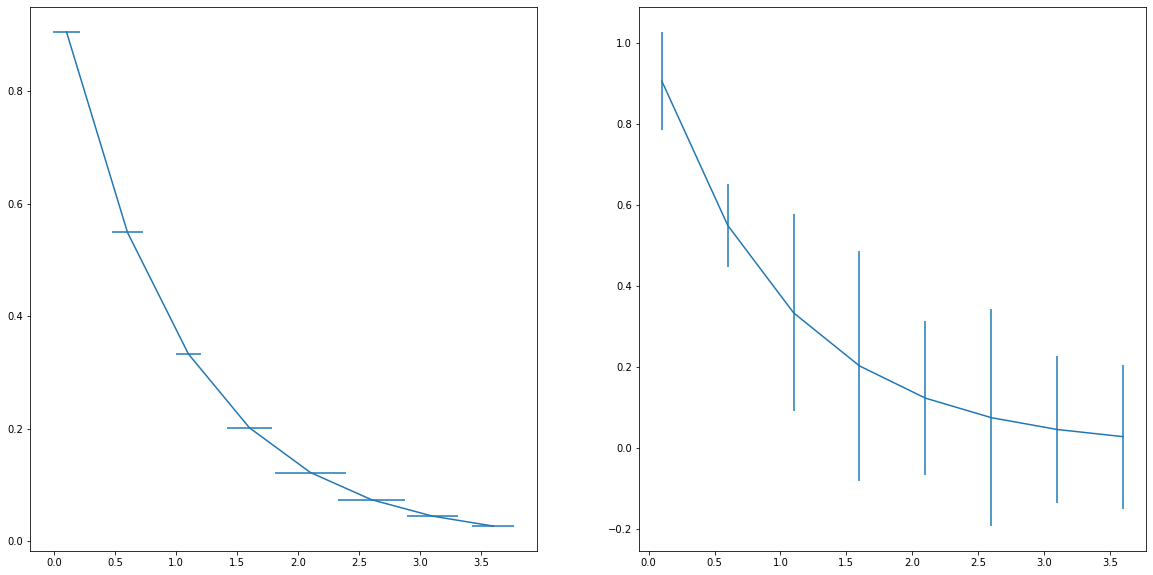
¿Cuándo utilizar gráfico de barra de error?
x: Dato del tipo posicional o cuantitativo.
y: Dato del tipo posicional o cuantitativo.
z: Dato del tipo posicional o cuantitativo.
Los valores de z tienen que tener las mismas unidades y.
Scatter Plot¶
El clásico gráfico de puntos
t = np.arange(0.0, 5.0, 0.1)
error = np.random.uniform(-2, 2, len(t))
fig, ax = plt.subplots(figsize=(10, 10))
ax.scatter(t, f(t) + error)
ax.grid(alpha=0.5)
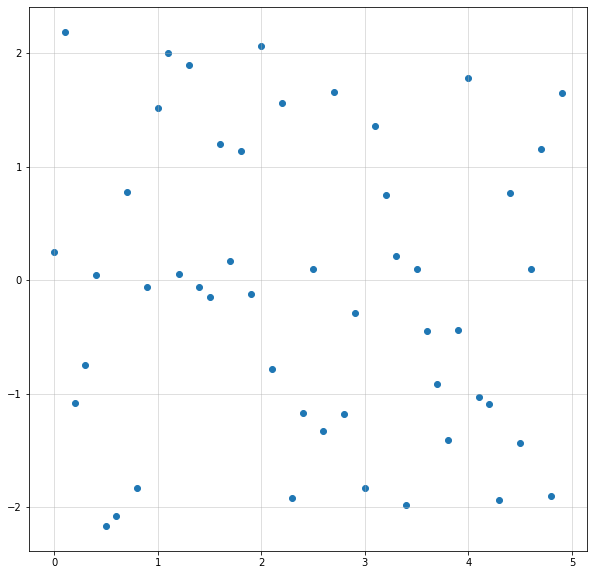
Incluso algunos más elaborados podría ser algo de este estilo.
N = 100
r0 = 0.6
x = 0.9 * np.random.rand(N)
y = 0.9 * np.random.rand(N)
area = np.pi * (10 * np.random.rand(N)) ** 2 # 0 to 10 point radiuses
c = np.sqrt(area)
r = np.sqrt(x ** 2 + y ** 2)
cm1 = plt.cm.get_cmap('RdYlBu')
cm2 = plt.cm.get_cmap('Greys')
plt.figure(figsize=(20, 12))
area1 = np.ma.masked_where(r < r0, area)
area2 = np.ma.masked_where(r >= r0, area)
sc1 = plt.scatter(x, y, s=area1, marker='^', c=c, cmap=cm1)
plt.colorbar(sc1)
sc2 = plt.scatter(x, y, s=area2, marker='o', c=c, cmap=cm2)
plt.colorbar(sc2)
# Show the boundary between the regions:
theta = np.arange(0, np.pi / 2, 0.01)
plt.plot(r0 * np.cos(theta), r0 * np.sin(theta), "k:", lw=2.0)
plt.show()
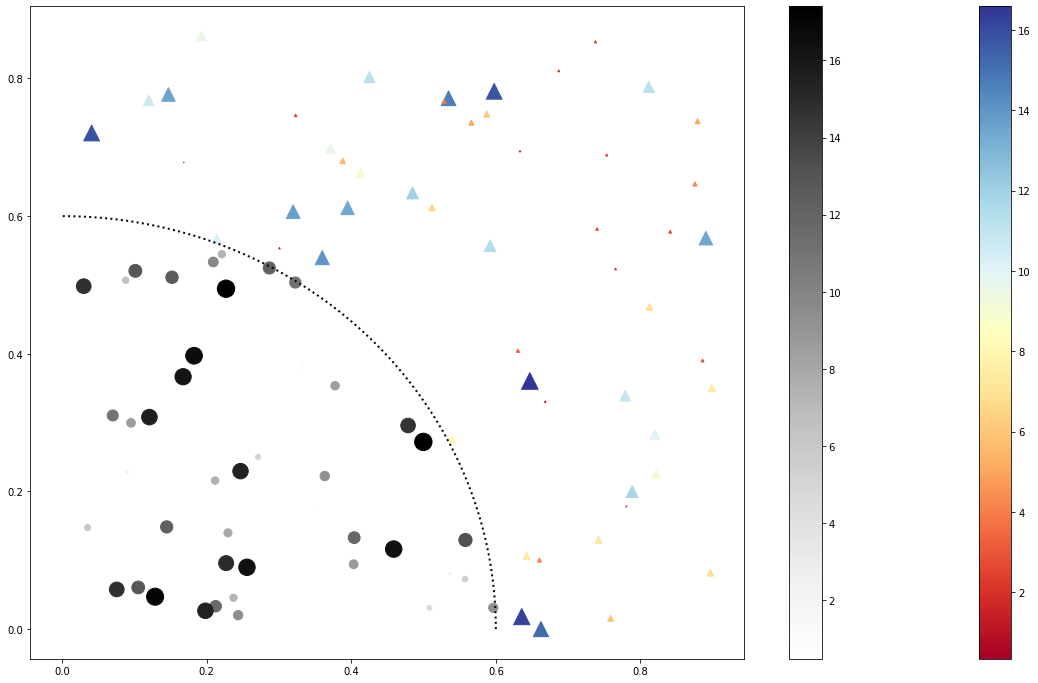
¿Cuándo utilizar scatter plot?
x: Dato del tipo posicional o cuantitativo.
y: Dato del tipo posicional o cuantitativo.
z: Dato del tipo nominal u ordinal (opcional)
Observación: Si hay pocos puntos, también puede usarse para z datos de tipo posicional o cuantitativo.
Countor Plot¶
x, y = np.mgrid[-3:3:.025, -2:2:.025]
pos = np.empty(x.shape + (2,))
pos[:, :, 0] = x
pos[:, :, 1] = y
z1 = multivariate_normal.pdf(
pos,
mean=[-1.0, -1.0],
cov=[[1.0, 0.0], [0.0, 0.1]]
)
z2 = multivariate_normal.pdf(
pos,
mean=[1.0, 1.0],
cov=[[1.5, 0.0], [0.0, 0.5]]
)
z = 10 * (z1 - z2)
fig, axs = plt.subplots(ncols=2, figsize=(20, 10), sharex=True, sharey=True)
cmaps = [cm.rainbow, cm.autumn, cm.coolwarm, cm.gray]
countour_styles = [
{"colors": "k", "linestyles": "solid"},
{"colors": "k", "linestyles": "dashed"},
]
for i, ax in zip(range(len(cmaps)), axs.ravel()):
cs = ax.contour(x, y, z, 11, **countour_styles[i])
if i > 0:
ax.clabel(cs, fontsize=9, inline=1)
ax.grid(alpha=0.5)
fig.show()
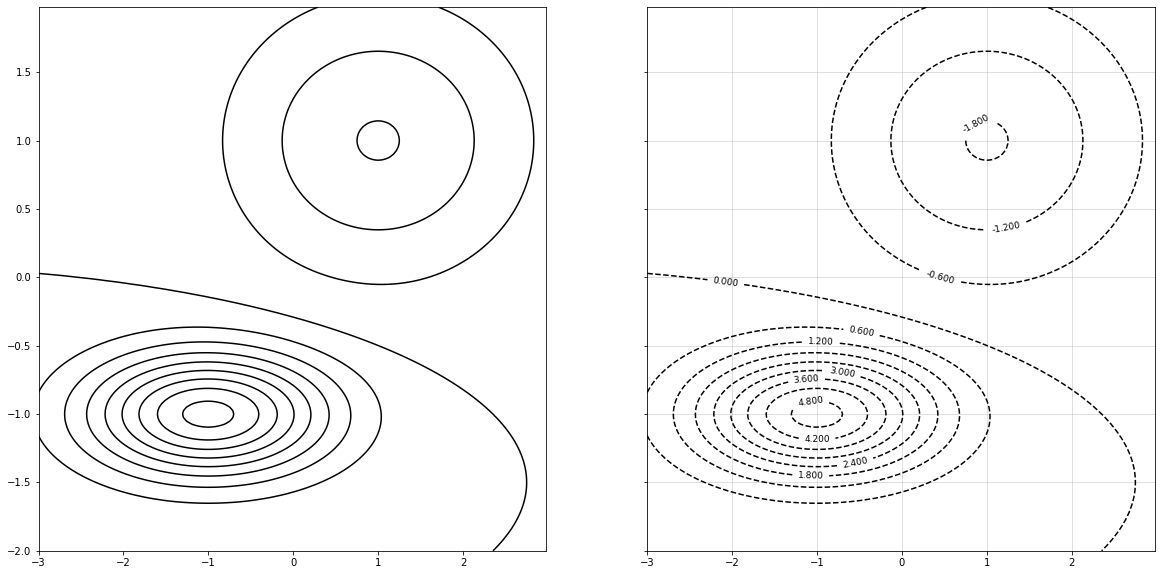
¿Cuándo se debe utiliar countour plot?
x: Dato del tipo posicional o cuantitativo.
y: Dato de tipo posicional o cuantitativo.
z: Dato de tipo posicional o cuantitativo.
Observación: Se debe tener suficiente densidad/regularidad de puntos como para poder obtener superficies de nivel.
Campos de Vectores¶
Algunos gráficos son mucho más específicos. Por ejemplo el campo de vectores es útil para observar flujos y sus magnitudes.
def my_vector_field():
X, Y = np.meshgrid(np.arange(0, 2 * np.pi, .2), np.arange(0, 2 * np.pi, .2))
U = np.cos(X)
V = np.sin(Y)
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(20, 10))
Q1 = ax1.quiver(U, V)
Q2 = ax2.quiver(
X[::3, ::3],
Y[::3, ::3],
U[::3, ::3],
V[::3, ::3],
pivot='mid',
color='r',
units='inches'
)
ax2.plot(X[::3, ::3], Y[::3, ::3], 'k.')
fig.show()
my_vector_field()
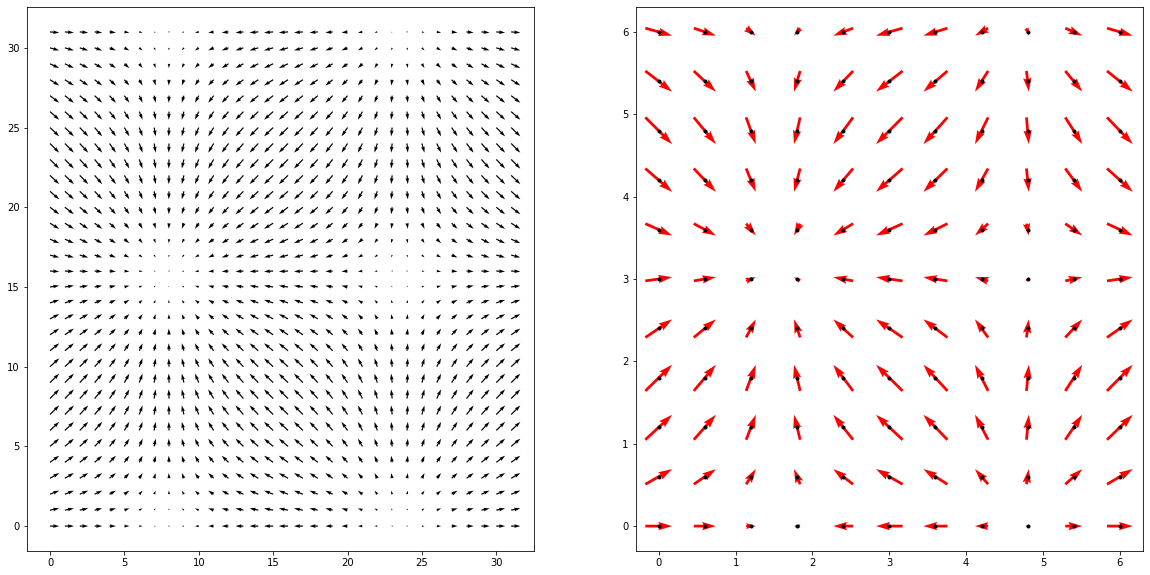
¿Cuándo utilizar campos de vectores?
x: Debe ser datos del tipo posicional o cuantitativo.
y: Debe ser datos de tipo posicional o cuantitativo.
z: Pendiente debe ser dato de tipo posicional o cuantitativo.
Evitar gráfico de campo de vectores si no es posible la interpretación correspondiente.
El límite es la imaginación¶
Puedes encontrar una infinidad de ejemplos en la Galería de Maplotlib (link).
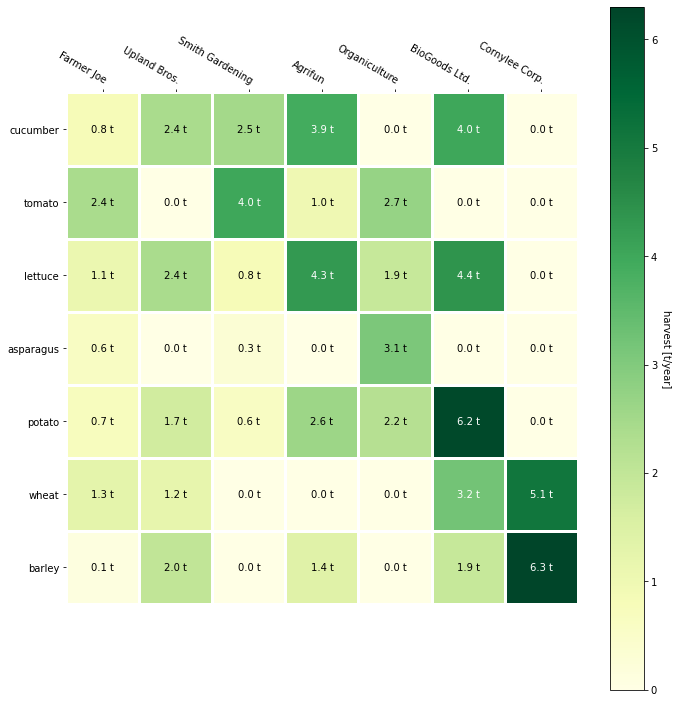
Mapas de Calor¶
from mpl_heatmap import heatmap, annotate_heatmap
vegetables = ["cucumber", "tomato", "lettuce", "asparagus",
"potato", "wheat", "barley"]
farmers = ["Farmer Joe", "Upland Bros.", "Smith Gardening",
"Agrifun", "Organiculture", "BioGoods Ltd.", "Cornylee Corp."]
harvest = np.array([[0.8, 2.4, 2.5, 3.9, 0.0, 4.0, 0.0],
[2.4, 0.0, 4.0, 1.0, 2.7, 0.0, 0.0],
[1.1, 2.4, 0.8, 4.3, 1.9, 4.4, 0.0],
[0.6, 0.0, 0.3, 0.0, 3.1, 0.0, 0.0],
[0.7, 1.7, 0.6, 2.6, 2.2, 6.2, 0.0],
[1.3, 1.2, 0.0, 0.0, 0.0, 3.2, 5.1],
[0.1, 2.0, 0.0, 1.4, 0.0, 1.9, 6.3]])
fig, ax = plt.subplots(figsize=(10, 10))
im, cbar = heatmap(harvest, vegetables, farmers, ax=ax,
cmap="YlGn", cbarlabel="harvest [t/year]")
texts = annotate_heatmap(im, valfmt="{x:.1f} t")
fig.tight_layout()
plt.show()
Conjunto de Mandelbrot¶
def mandelbrot_set(xmin, xmax, ymin, ymax, xn, yn, maxiter, horizon=2.0):
X = np.linspace(xmin, xmax, xn).astype(np.float32)
Y = np.linspace(ymin, ymax, yn).astype(np.float32)
C = X + Y[:, None] * 1j
N = np.zeros_like(C, dtype=int)
Z = np.zeros_like(C)
for n in range(maxiter):
I = abs(Z) < horizon
N[I] = n
Z[I] = Z[I]**2 + C[I]
N[N == maxiter-1] = 0
return Z, N
import time
import matplotlib
from matplotlib import colors
xmin, xmax, xn = -2.25, +0.75, 3000 // 2
ymin, ymax, yn = -1.25, +1.25, 2500 // 2
maxiter = 200
horizon = 2.0 ** 40
log_horizon = np.log2(np.log(horizon))
Z, N = mandelbrot_set(xmin, xmax, ymin, ymax, xn, yn, maxiter, horizon)
# Normalized recount as explained in:
# https://linas.org/art-gallery/escape/smooth.html
# https://www.ibm.com/developerworks/community/blogs/jfp/entry/My_Christmas_Gift
# This line will generate warnings for null values but it is faster to
# process them afterwards using the nan_to_num
with np.errstate(invalid='ignore'):
M = np.nan_to_num(N + 1 - np.log2(np.log(abs(Z))) + log_horizon)
dpi = 72
width = 10
height = 10*yn/xn
fig = plt.figure(figsize=(width, height), dpi=dpi)
ax = fig.add_axes([0, 0, 1, 1], frameon=False, aspect=1)
# Shaded rendering
light = colors.LightSource(azdeg=315, altdeg=10)
M = light.shade(M, cmap=plt.cm.hot, vert_exag=1.5,
norm=colors.PowerNorm(0.3), blend_mode='hsv')
ax.imshow(M, extent=[xmin, xmax, ymin, ymax], interpolation="bicubic")
ax.set_xticks([])
ax.set_yticks([])
# Some advertisement for matplotlib
year = time.strftime("%Y")
text = ("The Mandelbrot fractal set\n"
"Rendered with matplotlib %s, %s - http://matplotlib.org"
% (matplotlib.__version__, year))
ax.text(xmin+.025, ymin+.025, text, color="white", fontsize=12, alpha=0.5)
plt.show()