Parameter Estimation#
Now, let’s consider another scenario. Imagine another researcher sampled data every day, \(x_{observed} = (x(t_1), x(t_2) , \ldots, x(t_n))\) and \(y_{observed} = (y(t_1), y(t_2) , \ldots, y(t_n))\) where \(t_1, t_2, \ldots, t_n\) represents time. The goal here is to determine the best values \(\alpha\), \(\beta\), \(\gamma\) and \(\delta\) for this sampled data. $\( \dfrac{dx}{dt} = \alpha x - \beta xy \\ \dfrac{dy}{dt} = -\gamma y + \delta xy \)$ This is called an Inverse Problem but some authors also called this sort of approaches as Data-Driven Discovery. We will use PINNs for this purpose and you will notice we only need to add some extra features compared to the last lesson.
import re
import numpy as np
import matplotlib.pyplot as plt
import deepxde as dde
from scipy.integrate import solve_ivp
from deepxde.backend import tf
2023-06-05 03:29:49.227392: I tensorflow/tsl/cuda/cudart_stub.cc:28] Could not find cuda drivers on your machine, GPU will not be used.
2023-06-05 03:29:49.278496: I tensorflow/tsl/cuda/cudart_stub.cc:28] Could not find cuda drivers on your machine, GPU will not be used.
2023-06-05 03:29:49.279161: I tensorflow/core/platform/cpu_feature_guard.cc:182] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 AVX512F FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
2023-06-05 03:29:50.051011: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT
Using backend: tensorflow.compat.v1
Other supported backends: tensorflow, pytorch, jax, paddle.
paddle supports more examples now and is recommended.
WARNING:tensorflow:From /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/compat/v2_compat.py:107: disable_resource_variables (from tensorflow.python.ops.variable_scope) is deprecated and will be removed in a future version.
Instructions for updating:
non-resource variables are not supported in the long term
WARNING:tensorflow:From /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/deepxde/nn/initializers.py:118: The name tf.keras.initializers.he_normal is deprecated. Please use tf.compat.v1.keras.initializers.he_normal instead.
Training Data#
The train data will be generated by ourserlves, so we will have a better understading of the error. Let’s choose a time interval, initial conditions and parameters.
t_initial, t_final = 0, 10 # Equivalent to 10 days
x0 = 1.2
y0 = 0.8
alpha_real = 2 / 3
beta_real = 4 / 3
gamma_real = 1
delta_real = 1
parameters_real = {
"alpha": alpha_real,
"beta": beta_real,
"gamma": gamma_real,
"delta": delta_real
} # We will use this later for study errors
We can use a similar approach than last module for generate synthetic data, this will allows us to study errors.
def generate_data(
t,
x0,
y0,
alpha,
beta,
gamma,
delta
):
def func(t, Y):
x, y = Y
dx_dt = alpha * x - beta * x * y
dy_dt = - gamma * y + delta * x * y
return dx_dt, dy_dt
Y0 = [x0, y0]
t = t.flatten()
t_span = (t[0], t[-1])
sol = solve_ivp(func, t_span, Y0, t_eval=t)
return sol.y.T
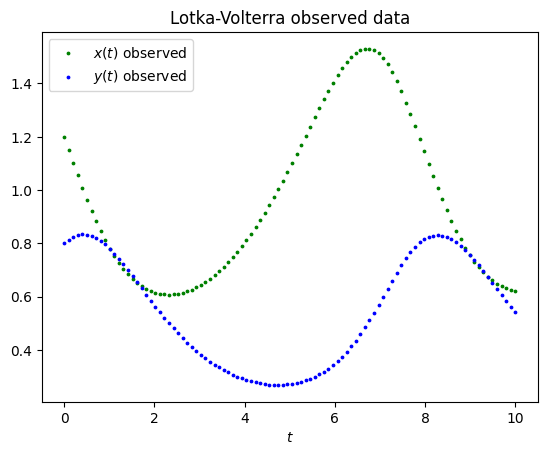
Generate the synthetic data and plot it.
t_train = np.linspace(t_initial, t_final, 100).reshape(-1, 1)
Y_train = generate_data(t_train, x0, y0, alpha_real, beta_real, gamma_real, delta_real)
x_train = Y_train[:, 0:1]
y_train = Y_train[:, 1:2]
plt.scatter(t_train, x_train, color="green", s=3, label=r"$x(t)$ observed")
plt.scatter(t_train, y_train, color="blue", s=3, label=r"$y(t)$ observed")
plt.legend()
plt.title("Lotka-Volterra observed data")
plt.xlabel(r"$t$")
plt.show()
PINNs Data-Driven Discovery#
Now we will forget for a minute about the real values of \(\alpha\), \(\beta\), \(\gamma\) and \(\delta\) since the goal of this lesson is to learn how to estimate these parameters. Let’s start defining them in a way that our code knows they have to be learned.
# Pick some initial guess
alpha = dde.Variable(0.0)
beta = dde.Variable(0.0)
gamma = dde.Variable(0.0)
delta = dde.Variable(0.0)
Now we have to define the residuals and initial conditions in the same way the forward approximation (previous module).
def ode(t, Y):
x = Y[:, 0:1]
y = Y[:, 1:2]
dx_dt = dde.grad.jacobian(Y, t, i=0)
dy_dt = dde.grad.jacobian(Y, t, i=1)
return [
dx_dt - alpha * x + beta * x * y,
dy_dt + gamma * y - delta * x * y
]
And also geometry and initial conditions
geom = dde.geometry.TimeDomain(t_initial, t_final)
def boundary(_, on_initial):
return on_initial
ic_x = dde.icbc.IC(geom, lambda x: x0, boundary, component=0)
ic_y = dde.icbc.IC(geom, lambda x: y0, boundary, component=1)
We can use the observed data t_train and Y_train, which are equivalent to \(x_{observed} = (x(t_1), x(t_2) , \ldots, x(t_n))\) and \(y_{observed} = (y(t_1), y(t_2) , \ldots, y(t_n))\) for learning the values of our parameters. So we need to declare a new object and then include it to our model.
observe_x = dde.icbc.PointSetBC(t_train.reshape(-1, 1), Y_train[:, 0:1], component=0)
observe_y = dde.icbc.PointSetBC(t_train.reshape(-1, 1), Y_train[:, 1:2], component=1)
Be careful! Note that component=0 is associated with the variable \(x\) every time, defining the gradients, initial conditions and observed data. Same for component=1 which corresponds to the variable \(y\).
The data object is similar but we include the observed data as well in the list of conditions. But also note that we can add the observed data as train points with the argument anchors.
data = dde.data.PDE(
geom,
ode,
[ic_x, ic_y, observe_x, observe_y],
num_domain=512,
num_boundary=2,
anchors=t_train,
)
Now we can define our neural network
neurons = 64
layers = 6
activation = "tanh"
initializer = "Glorot normal"
net = dde.nn.FNN([1] + [neurons] * layers + [2], activation, initializer)
Training#
This step is also similar, except we have to tell our model it has to learn external variables (\(\alpha\), \(\beta\), \(\gamma\) and \(\delta\)) using external_trainable_variables.
model = dde.Model(data, net)
model.compile(
"adam",
lr=0.001,
external_trainable_variables=[alpha, beta, gamma, delta]
)
Compiling model...
Warning: For the backend tensorflow.compat.v1, `external_trainable_variables` is ignored, and all trainable ``tf.Variable`` objects are automatically collected.
Building feed-forward neural network...
'build' took 0.077048 s
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/deepxde/nn/tensorflow_compat_v1/fnn.py:116: UserWarning: `tf.layers.dense` is deprecated and will be removed in a future version. Please use `tf.keras.layers.Dense` instead.
return tf.layers.dense(
'compile' took 0.568617 s
In order to study the convergence of the learning process related to the parameters we want to estimate we need a separate file where we can store these estimations. The file variables.dat will store ours estimations of \(\alpha\), \(\beta\), \(\gamma\) and \(\delta\) each 100 iterations.
variable = dde.callbacks.VariableValue(
[alpha, beta, gamma, delta],
period=100,
filename="variables.dat"
)
Do not forget to add this variable in the training process using callbacks=[variable].
losshistory, train_state = model.train(iterations=30000, display_every=5000, callbacks=[variable])
dde.utils.external.plot_loss_history(losshistory)
Training model...
2023-06-05 03:29:53.100229: I tensorflow/compiler/mlir/mlir_graph_optimization_pass.cc:353] MLIR V1 optimization pass is not enabled
Step Train loss Test loss Test metric
0 [1.04e-04, 1.24e-03, 1.44e+00, 6.40e-01, 9.25e-01, 2.47e-01] [1.04e-04, 1.24e-03, 1.44e+00, 6.40e-01, 9.25e-01, 2.47e-01] []
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[13], line 1
----> 1 losshistory, train_state = model.train(iterations=30000, display_every=5000, callbacks=[variable])
2 dde.utils.external.plot_loss_history(losshistory)
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/deepxde/utils/internal.py:22, in timing.<locals>.wrapper(*args, **kwargs)
19 @wraps(f)
20 def wrapper(*args, **kwargs):
21 ts = timeit.default_timer()
---> 22 result = f(*args, **kwargs)
23 te = timeit.default_timer()
24 if config.rank == 0:
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/deepxde/model.py:633, in Model.train(self, iterations, batch_size, display_every, disregard_previous_best, callbacks, model_restore_path, model_save_path, epochs)
631 if iterations is None:
632 raise ValueError("No iterations for {}.".format(self.opt_name))
--> 633 self._train_sgd(iterations, display_every)
634 self.callbacks.on_train_end()
636 if config.rank == 0:
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/deepxde/model.py:651, in Model._train_sgd(self, iterations, display_every)
646 self.callbacks.on_batch_begin()
648 self.train_state.set_data_train(
649 *self.data.train_next_batch(self.batch_size)
650 )
--> 651 self._train_step(
652 self.train_state.X_train,
653 self.train_state.y_train,
654 self.train_state.train_aux_vars,
655 )
657 self.train_state.epoch += 1
658 self.train_state.step += 1
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/deepxde/model.py:540, in Model._train_step(self, inputs, targets, auxiliary_vars)
538 if backend_name == "tensorflow.compat.v1":
539 feed_dict = self.net.feed_dict(True, inputs, targets, auxiliary_vars)
--> 540 self.sess.run(self.train_step, feed_dict=feed_dict)
541 elif backend_name in ["tensorflow", "paddle"]:
542 self.train_step(inputs, targets, auxiliary_vars)
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/client/session.py:968, in BaseSession.run(self, fetches, feed_dict, options, run_metadata)
965 run_metadata_ptr = tf_session.TF_NewBuffer() if run_metadata else None
967 try:
--> 968 result = self._run(None, fetches, feed_dict, options_ptr,
969 run_metadata_ptr)
970 if run_metadata:
971 proto_data = tf_session.TF_GetBuffer(run_metadata_ptr)
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/client/session.py:1191, in BaseSession._run(self, handle, fetches, feed_dict, options, run_metadata)
1188 # We only want to really perform the run if fetches or targets are provided,
1189 # or if the call is a partial run that specifies feeds.
1190 if final_fetches or final_targets or (handle and feed_dict_tensor):
-> 1191 results = self._do_run(handle, final_targets, final_fetches,
1192 feed_dict_tensor, options, run_metadata)
1193 else:
1194 results = []
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/client/session.py:1371, in BaseSession._do_run(self, handle, target_list, fetch_list, feed_dict, options, run_metadata)
1368 return self._call_tf_sessionprun(handle, feed_dict, fetch_list)
1370 if handle is None:
-> 1371 return self._do_call(_run_fn, feeds, fetches, targets, options,
1372 run_metadata)
1373 else:
1374 return self._do_call(_prun_fn, handle, feeds, fetches)
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/client/session.py:1378, in BaseSession._do_call(self, fn, *args)
1376 def _do_call(self, fn, *args):
1377 try:
-> 1378 return fn(*args)
1379 except errors.OpError as e:
1380 message = compat.as_text(e.message)
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/client/session.py:1361, in BaseSession._do_run.<locals>._run_fn(feed_dict, fetch_list, target_list, options, run_metadata)
1358 def _run_fn(feed_dict, fetch_list, target_list, options, run_metadata):
1359 # Ensure any changes to the graph are reflected in the runtime.
1360 self._extend_graph()
-> 1361 return self._call_tf_sessionrun(options, feed_dict, fetch_list,
1362 target_list, run_metadata)
File /opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/tensorflow/python/client/session.py:1454, in BaseSession._call_tf_sessionrun(self, options, feed_dict, fetch_list, target_list, run_metadata)
1452 def _call_tf_sessionrun(self, options, feed_dict, fetch_list, target_list,
1453 run_metadata):
-> 1454 return tf_session.TF_SessionRun_wrapper(self._session, options, feed_dict,
1455 fetch_list, target_list,
1456 run_metadata)
KeyboardInterrupt:
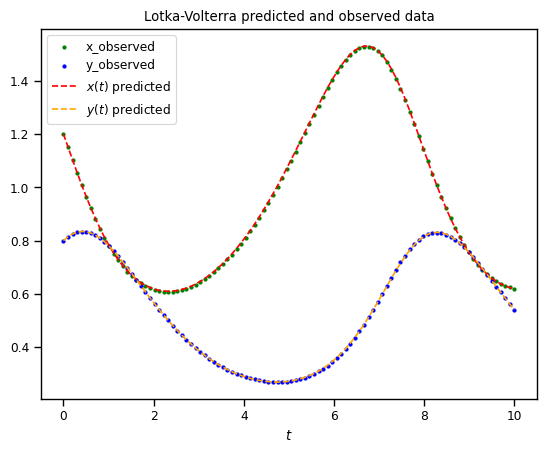
We can plot the data as well but it is not the main point of this lesson.
plt.scatter(t_train, x_train, color="green", s=5, label="x_observed")
plt.scatter(t_train, y_train, color="blue", s=5, label="y_observed")
sol_pred = model.predict(t_train.reshape(-1, 1))
x_pred = sol_pred[:, 0:1]
y_pred = sol_pred[:, 1:2]
plt.plot(t_train, x_pred, color="red", linestyle="dashed", label=r"$x(t)$ predicted")
plt.plot(t_train, y_pred, color="orange", linestyle="dashed", label=r"$y(t)$ predicted")
plt.legend()
plt.title("Lotka-Volterra predicted and observed data")
plt.xlabel(r"$t$")
plt.show()
Learning History#
We need to open the file variables.dat and create arrays for each parameter. Do not worry about the next piece of code, it will only return a dictionary where keys are the name of the parameters and values are their learning history.
lines = open("variables.dat", "r").readlines()
raw_parameters_pred_history = np.array(
[
np.fromstring(
min(re.findall(re.escape("[") + "(.*?)" + re.escape("]"), line), key=len),
sep=",",
)
for line in lines
]
)
iterations = [int(re.findall("^[0-9]+", line)[0]) for line in lines]
parameters_pred_history = {
name: raw_parameters_pred_history[:, i]
for i, name in enumerate(parameters_real.keys())
}
parameters_pred_history.keys()
dict_keys(['alpha', 'beta', 'gamma', 'delta'])
n_callbacis, n_variables = raw_parameters_pred_history.shape
fig, axes = plt.subplots(nrows=n_variables, sharex=True)
for ax, (parameter, parameter_value) in zip(axes, parameters_real.items()):
ax.plot(iterations, parameters_pred_history[parameter] , "-")
ax.plot(iterations, np.ones_like(iterations) * parameter_value, "--")
ax.set_ylabel(parameter)
ax.set_xlabel("Iterations")
fig.suptitle("Parameter estimation")
fig.tight_layout()
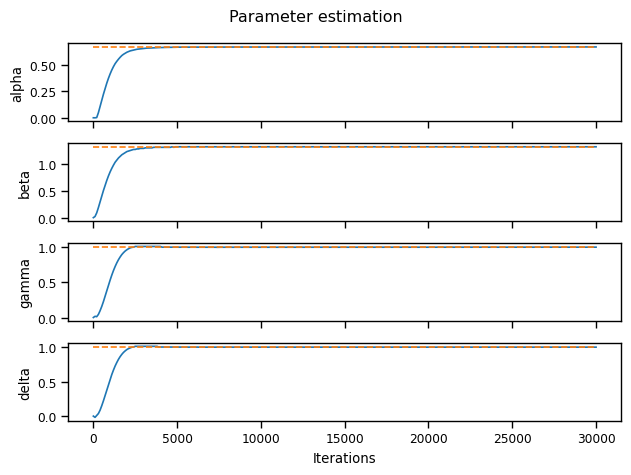
It took less than 5000 iterations to get a really good approximation for each variable! Now we can calculate the relative error for each parameter since we already know the real value.
alpha_pred, beta_pred, gamma_pred, delta_pred = variable.value
print(f"alpha - real: {alpha_real:4f} - predicted: {alpha_pred:4f} - relative error: {np.abs((alpha_real - alpha_pred) / alpha_real):4f}")
print(f"beta - real: {beta_real:4f} - predicted: {beta_pred:4f} - relative error: {np.abs((beta_real - beta_pred) / beta_real):4f}")
print(f"gamma - real: {gamma_real:4f} - predicted: {gamma_pred:4f} - relative error: {np.abs((gamma_real - gamma_pred) / gamma_real):4f}")
print(f"delta - real: {delta_real:4f} - predicted: {delta_pred:4f} - relative error: {np.abs((delta_real - delta_pred) / delta_real):4f}")
alpha - real: 0.666667 - predicted: 0.664968 - relative error: 0.002548
beta - real: 1.333333 - predicted: 1.330009 - relative error: 0.002493
gamma - real: 1.000000 - predicted: 0.999559 - relative error: 0.000441
delta - real: 1.000000 - predicted: 0.998377 - relative error: 0.001623